Abstract
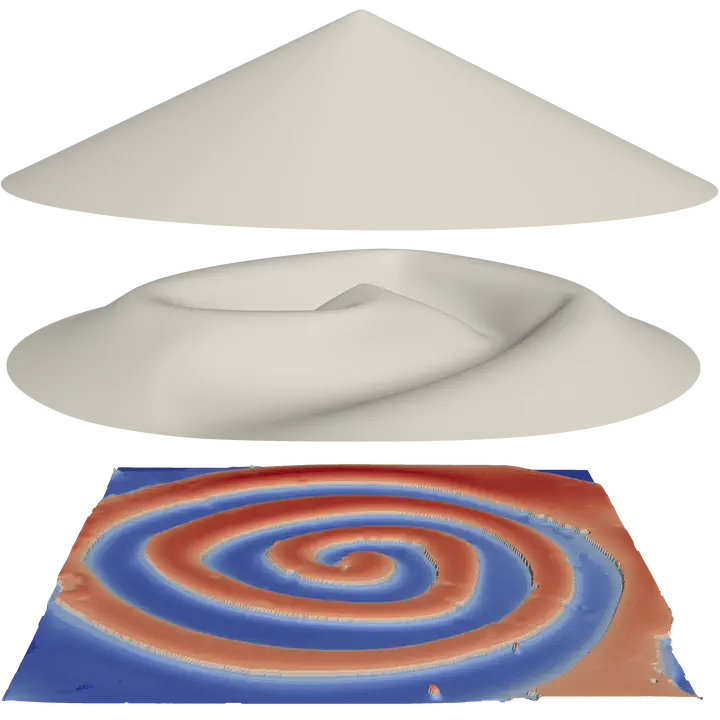
Liquid crystal elastomer films that morph into cones are strikingly capable lifters. Thus motivated, we combine theory, numerics, and experiments to reexamine the load-bearing capacity of conical shells. We show that a cone squashed between frictionless surfaces buckles at a smaller load, even in scaling, than the classical Seide/Koiter result. Such buckling begins in a region of greatly amplified azimuthal compression generated in an outer boundary layer with oscillatory bend. Experimentally and numerically, buckling then grows sub-critically over the full cone. We derive a new thin-limit formula for the critical load, ∝ t^(5/2), and validate it numerically. We also investigate deep post-buckling, finding further instabilities producing intricate states with multiple Pogorelov-type curved ridges arranged in concentric circles or Archimedean spirals. Finally, we investigate the forces exerted by such states, which limit lifting performance in active cones.