Abstract
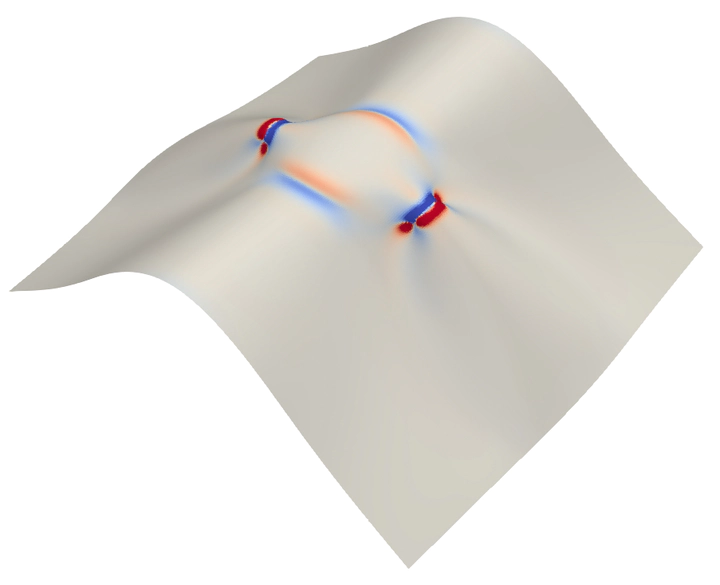
Liquid crystalline elastomers (LCEs) are shape-changing materials that exhibit large deformations in response to applied stimuli. Local control of the orientation of LCEs spatially directs the deformation of these materials to realize a spontaneous shape change in response to stimuli. Prior approaches to shape programming in LCEs utilize patterning techniques that involve the detailed inscription of spatially varying nematic fields to produce sheets. These patterned sheets deform into elaborate geometries with complex Gaussian curvatures. Here, we present an alternative approach to realize shape-morphing in LCEs where spatial patterning of the crosslink density locally regulates the material deformation magnitude on either side of a prescribed interface curve. We also present a simple mathematical model describing the behavior of these materials. Further experiments coupled with the mathematical model demonstrate the control of the sign of Gaussian curvature, which is used in combination with heat transfer effects to design LCEs that self-clean as a result of temperature-dependent actuation properties.